Unfolding Europe

I like couchsurfing from time to time. Not only is it a very good way to connect to the place you are visiting, but also to get to know interesting people outside your usual bubble and, thus, to learn new stuff. When I was in Sarajevo in 2019, my wonderful host told me an astonishing thing about Bosnia and Herzegovina:

It seems to be a small country. But if you unfold and flatten it, it’s actually larger than Europe.

I had just come to Sarajevo on a bus from Split in Croatia and I had seen rugged, mountainous landscapes on the way that offered some support for this claim. Nevertheless, I promised myself to have a look into the matter when back from the trip.

So, let’s unfold and flatten Bosnia and Herzegovina and compare its size with the area of Europe. Unfolding and flattening a country would probably mean to measure its surface area – as opposed to the usual horizontal (or: planar/planimetric) area. There are methods and tools for that task. But before getting out the spatial data science machinery for the analysis, some preliminary questions need to be clarified:

1. What is Europe?

That’s an old question. For pragmatic reasons, I will use EU-DEM elevation data for the analysis and define Europe in this context as all countries (almost) entirely covered by this data set. This excludes Russia, Ukraine, Belarus and others, but includes all of Turkey.

2. What is the area of Europe that will be compared to the surface area of Bosnia and Herzegovina?

There are other countries in Europe that have much to gain in surface area – think of Switzerland! And, first and foremost, Bosnia and Herzegovina is a part of Europe. By definition, it cannot be larger than Europe. The original claim is obviously about the surface area of Bosnia and Herzegovina being larger than the horizontal area of Europe. This means, we will be comparing apples and pears.

3. At what level of detail will the surface area be calculated?

Just as the length of a coastline, the surface area can never be well-defined. The calculated value of the surface area depends largely on the measurement resolution. I will use EU-DEM elevation data with a ground resolution of 25 m – because it is readily available for a Europe-wide analysis. Using more fine-grained data would probably result in larger values for the surface area.

I’ll use R with the raster and sf packages for spatial data processing, leaflet for an interactive visualisation of the slope dataset, and exactextractr for the extraction of aggregated values with a custom function to calculate the surface area. With rmapshaper, cartogram and gganimate, I’ll be able to visualise the effect of unfolding Europe.

require(tidyverse)
require(here)
require(glue)
require(raster)
require(sf)
require(mapview)
require(leaflet)
require(exactextractr)
require(DT)
require(gghighlight)
require(rmapshaper)
require(cartogram)
require(scales)
require(RColorBrewer)
require(gganimate)

require(conflicted)
conflict_prefer("filter", "dplyr")
conflict_prefer("select", "dplyr")
conflict_prefer("animate", "gganimate")

First of all, I acquire EU-DEM v1.0 slope data. The data set is available in a Lambert Equal-Area projection and split into 23 tiles:

wms <- "https://image.discomap.eea.europa.eu/arcgis/services/Elevation/Slope/MapServer/WmsServer?"

leaflet() %>% 
    addProviderTiles(providers$CartoDB.Positron) %>%
    addWMSTiles(
        wms, layers = "Image,Boundary,Downloads",
        options = WMSTileOptions(format = "image/png", transparent = T),
        attribution = "European Environment Agency (EEA)"
    ) %>% 
    setView(10, 55, zoom = 2)

You need to log in to get access to the tiles. I manually downloaded all the files, unzipped them and saved all the geotiffs into one folder. From there, I can access them with the raster function. I set zero as the NA value to avoid problems with the island of Jan Mayen – which is not covered by the EU-DEM data, but part of the Norwegian county of Nordland in the Natural Earth admin 1 boundary data.

eudem_slope <- here("../../data/eudem/slope/") %>%
    list.files(full.names = T, pattern = "tif$") %>%
    map(raster)

for(i in 1:length(eudem_slope)) NAvalue(eudem_slope[[i]]) <- 0

st_envelope <- function(r) st_as_sfc(st_bbox(r))  

envelope <- eudem_slope %>% 
    map(st_envelope) %>%
    reduce(st_union)

I want to know the surface area of European countries, but in the cartogram visualisation, I prefer to use even smaller geographical units for more detail. So, I’ll be using admin 1 boundaries from Natural Earth at a 1:10m scale to extract aggregated area values. Caveat: These boundary polygons are already quite generalised (e.g. very small islands are missing), so the extracted area values will be somewhat distorted.

I first use a spatial filter to retain only polygons that are entirely within the slope raster tiles. Then I explicitly remove sub-national units of a number of countries that are not covered by EU-DEM data.

ne <- "ne_10m_admin_1_states_provinces_lakes"

exclude <- c(
    "ARM", "AZE", "BLR", "DZA", "EGY", "GEO", "IRN", "IRQ", "ISR", "JOR",
    "LBN", "LBY", "MAR", "MDA", "RUS", "SYR", "TUN", "UKR"
)

adm1 <- here(glue("../../data/natural_earth/{ne}/{ne}.shp")) %>%
    read_sf() %>%
    st_transform(st_crs(envelope)) %>%
    st_filter(envelope, .predicate = st_within) %>%
    filter(!(sov_a3 %in% exclude))

Probably the simplest way to calculate surface area is to divide the planar area by the cosine of the slope angle. This is – compared to other methods – a rather approximate way, but it scales well and will be good enough for this particular purpose:

\(\text{surface area} = \frac{\text{planar area}}{\cos{slope}}\)

When looking into the conversion table provided with the slope data, there is the pleasant discovery that its DN is actually already encoded as cosine of the slope (times 250):

slope[degrees] = float(acos(DN/250)*180/!PI)

This makes it even easier for us! The following function can be used by exactextractr to aggregate the horizontal and surface area from the EU-DEM slope data accordingly:

eudem_slope_to_area <- function(slope, coverage_fraction, res = 25, ...) { 
    
    data.frame(
        horizontal = sum(coverage_fraction * res^2, na.rm = T), 
        surface = sum((coverage_fraction * res^2) / (slope/250), na.rm = T)
    )
}

The following processing chain extracts aggregated values from all 23 raster tiles for the boundary polygons, summarises the data on the admin 1 units and calculates a ratio of the surface to the horizontal area:

extract_surface_area <- function(x, y) {
    y <- st_filter(y, st_as_sfc(st_bbox(x)))
    exact_extract(x, y, eudem_slope_to_area, append_cols = "adm1_code", progress = F)
}

surface_area <- eudem_slope %>%
    map(extract_surface_area, adm1) %>%
    reduce(rbind) %>%
    filter(surface > 0) %>%
    group_by(adm1_code) %>%
    summarise(
        horizontal = sum(horizontal), 
        surface = sum(surface), 
        ratio = surface/horizontal
    ) %>%
    left_join(adm1) %>%
    st_sf()

Let’s have a look on the results of the calculation. Here are all the sub-national geographical units with their horizontal and surface area, ordered by excess area – the percentage difference of surface and horizontal area:

surface_area %>% 
    transmute(
        name, admin, 
        horizontal_sqkm = horizontal/1e6, surface_sqkm = surface/1e6, 
        excess = ratio-1
    ) %>%
    st_drop_geometry() %>%
    arrange(desc(excess)) %>%
    datatable(
        colnames = c(
            "Admin Name", "Country", 
            "Horizontal Area (sqkm)", "Surface Area (sqkm)", "Excess Area"
        ),
        filter = "top",
        options = list(pageLength = 10, scrollX = T)
    ) %>%
    formatRound(3:4, digits = 2) %>%
    formatPercentage(5, digits = 4)

I thought it would be a clever idea to use a cartogram to visualise the surface area. In an equal-area map, the area of objects on the map is proportional to the area of the objects in reality. In a cartogram, however, the area of objects on the map is used to encode other variables such as population. It seems thus very fitting to use area on the map to encode surface area.

I use the cartogram package to create new geometries for the admin 1 boundary polygons. The proportions of the areas of the new geometries will correspond to their surface areas:

simplified <- surface_area %>% 
    ms_simplify() %>%
    mutate(adm1_code, surface, ratio)

cartogram_sf <- simplified %>%
    mutate(type = "Horizontal Area") %>%
    rbind(
       simplified %>%
            mutate(type = "Surface Area") %>%
            cartogram_cont("surface", itermax = 25)
    )

In order to show the difference between horizontal and surface area, gganimate can be used to make an animation with smooth transitions between the map and the cartogram:

colours <- brewer.pal(7, "YlOrBr")[2:7]

labels <- c(
    " 0 \U2012  <1",
    " 1 \U2012  <2",
    " 2 \U2012  <4",
    " 4 \U2012  <8",
    " 8 \U2012 <16",
    "16 \U2012  23"
)    

animation <- cartogram_sf %>%
    mutate(bin = cut(ratio-1, breaks = c(0, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32))) %>%
    ggplot() +
    geom_sf(aes(fill = bin, group = adm1_code), size = 0, color = NA) +
    scale_fill_manual(name = "% Excess Area", values = colours, labels = labels) +
    labs(title = "{closest_state}") +
    theme_minimal() +
    theme(
        text = element_text(family = "mono"),
        legend.position = c(0.85, 0.7),
        legend.title = element_text(size = rel(1.3)),
        legend.text = element_text(size = rel(1.3)), 
        legend.text.align = 1,
        plot.title.position = "plot",
        plot.title = element_text(face = "bold", size = rel(1.3), hjust = .5)
    ) +
    transition_states(type) + 
    ease_aes("cubic-in-out")
    

gif <- here("static/img/portfolio/unfolding-europe/unfolding-europe.gif")

animation %>% animate(
    duration = 5, start_pause = 0, end_pause = 15, 
    device = "ragg_png", renderer = gifski_renderer(file = gif), 
    width = 800, height = 600, unit = "px"
)

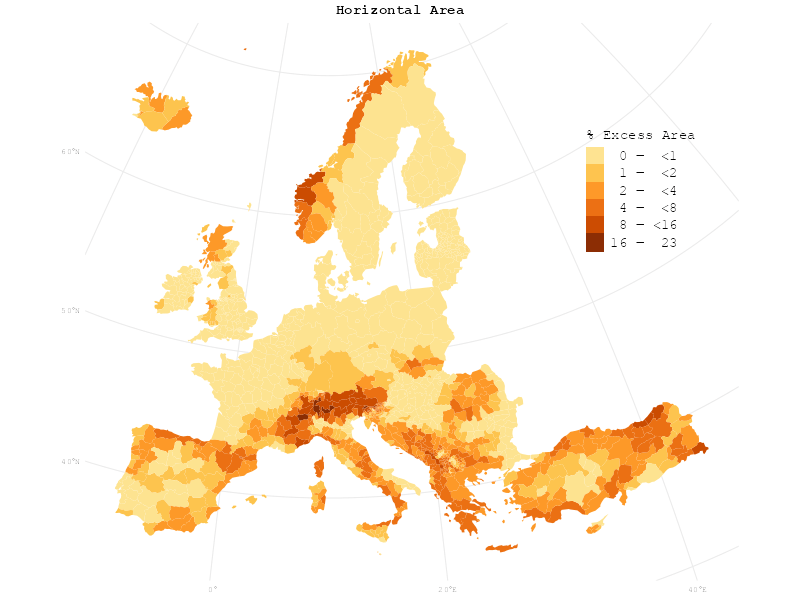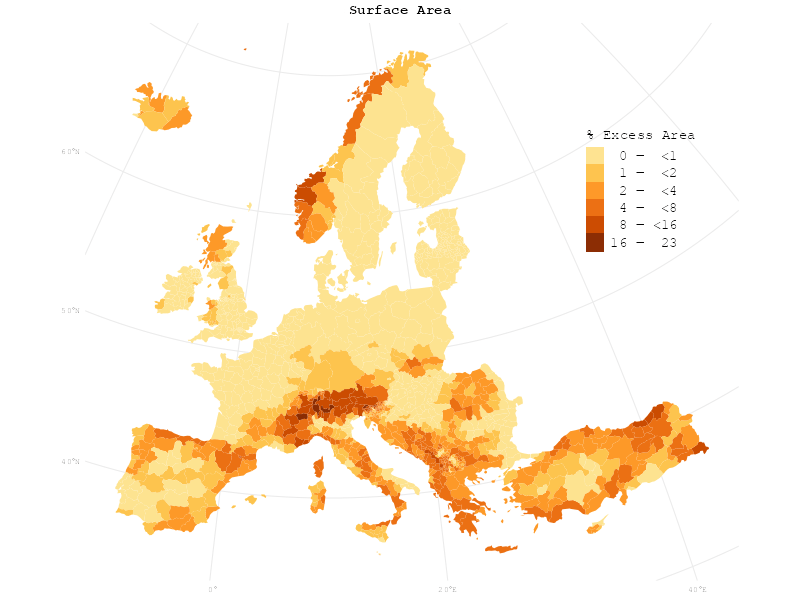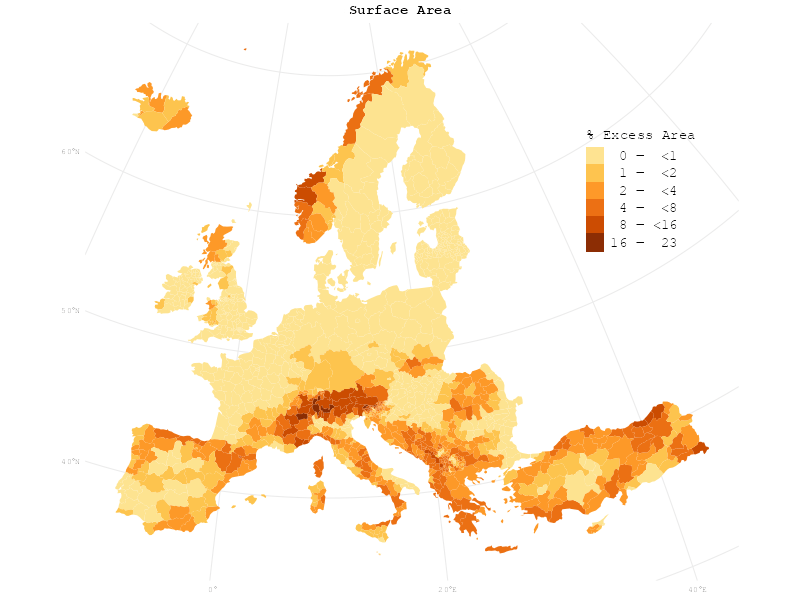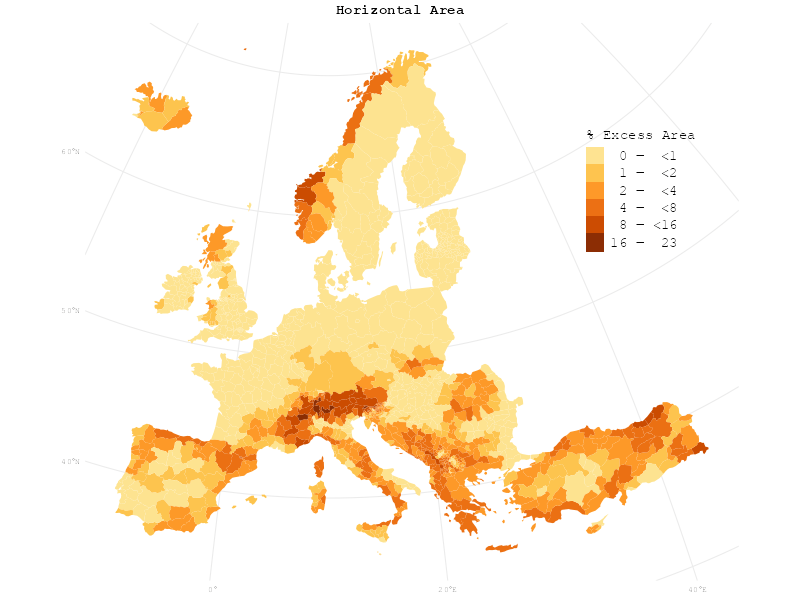
Can you see it? Horizontal and surface area are not as radically different from each other as the original claim of Bosnia and Herzegovina’s hidden size would suggest – you have to look very closely to actually notice the change.

So what about Bosnia and Herzegovina after all? Let’s have a look at the surface area of countries:

by_country <- surface_area %>% 
    group_by(admin) %>%
    summarise(
        horizontal = sum(horizontal),
        surface = sum(surface), 
        excess = (surface/horizontal)-1,
    )

Bosnia and Herzegovina has – according to this analysis with all its inherent limitations – a surface area of 53,557.52 sqkm. This corresponds to 0.9% of the total horizontal area of all the European countries in the data set. In conclusion, the analysis does not support the claim that Bosnia and Herzegovina would be larger than Europe if flattened out.

After all, it ranks as number 14 out of 51 countries regarding the excess area. Quite as expected, Switzerland is the territorial state in Europe that proportionally gains the most by unfolding its area:

by_country %>%
    ggplot(aes(y = reorder(admin, excess), x = excess)) +
    geom_col(fill = "firebrick") +
    scale_x_continuous(labels = label_percent(accuracy = 1)) +
    labs(x = "Excess area", y = NULL) +
    gghighlight(admin == "Bosnia and Herzegovina") +
    theme_minimal()